Versions
- 2022-02-07 (2)
- 2021-09-17 (1)
How to Cite
Copyright notice
This work is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License.
Copyright (c) 2021 Rayanne A. Luke, Richard J. Braun, Carolyn G. Begley
Keywords
Abstract
Purpose: Little quantitative or mechanistic information about tear film breakup can be determined directly via current imaging techniques. In this paper, we present simplified mathematical models based on two proposed mechanisms of tear film breakup: evaporation of water from the tear film and tangential fluid flow within the tear film. We use our models to determine whether one or a combination of the two mechanisms causes tear film breakup in a variety of instances. In this study, we estimate related breakup parameters that cannot currently be measured in breakup during subject trials, such as tear film osmolarity and thinning rates. The present study validates our procedure against previous work.
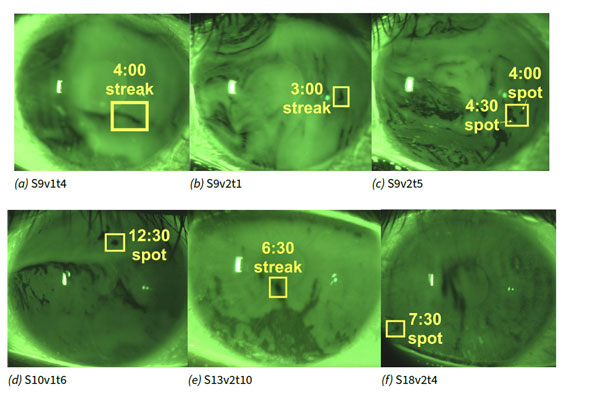
Methods: Five ordinary differential equation models for tear film thinning were designed that model evaporation, osmosis, and various types of tangential flow. Eight tear film breakup instances occurring within a time interval of 1–8 s postblink of five healthy subjects thatwere identified in fluorescence images in previous work were fit with these five models. The fitting procedure used a nonlinear least squares optimization that minimized the difference of the computed theoretical fluorescent intensity from the models and the experimental fluorescent intensity from the images. The optimization was conducted over the evaporation rate and up to three tangential flow rate parameters. The smallest norm of the difference was determined to correspond to the model that best explained the tear film dynamics.
Results: All of the breakup instances were best fit by models with time-dependent tangential flow. Our optimal parameter values and thinning rate as well as tangential fluid flow profiles compare well with previous partial differential equation model results in most instances.
Conclusion: Our fitting results suggest that a combination of tangential fluid flow and evaporation cause most of the breakup instances. Comparison with results from previous work suggests that the simplified models can capture the essential tear film dynamics in most cases, thereby validating this procedure for wider usage.
References
Norn M. Desiccation of the Precorneal Film: I. CornealWetting-Time. Acta Ophthalmol, 1969;47(4): 865–880.
Lemp MA et al. The definition and classification of dry eye disease: Report of the Definition and Classification Subcommittee of the International Dry Eye WorkShop. Ocul Surf, 2007;5, 75–92.
Willcox MDP, Argüeso P, Georgiev GA, Holopainen JM, Laurie GW, Millar TJ, et al. The TFOS DEWS II Tear Film Report. Ocul Surf, 2017;15, 369–406.
King-Smith PE, Begley CG, Braun RJ. Mechanisms, imaging and structure of tear film breakup. Ocul Surf, 2018;16, 4–30.
King-Smith PE, Hinel EA, Nichols JJ. Application of a novel interferometric method to investigate the relation between lipid layer thickness and tear film thinning. Invest Ophthalmol Vis Sci, 2010;51(5): 2418–2423.
Zhong L, Braun RJ, Begley CG, King-Smith PE. Dynamics of fluorescent imaging for rapid tear thinning. Bull Math Biol, 2019;81(1): 39–80.
Yokoi N, Georgiev GA. Tear-film-oriented diagnosis and therapy for dry eye. Dry eye syndrome: basic and clinical perspectives. Ed. by N Yokoi. London: Future Medicine, 2013; 96–108.
Yokoi N, Georgiev GA. Tear-film-oriented diagnosis for dry eye. Jpn J Ophthalmol, 2019;63, 127–136.
Berger R, Corrsin S. A surface tension gradient mechanism for driving the pre-corneal tear film after a blink. J Biomech, 1974;7, 225–38.
Craster RV, Matar OK. Dynamics and stability of thin liquid films. Rev Mod Phys, 2009;81(3): 1131.
Sharma A, Ruckenstein E. Mechanism of Tear Film Rupture and Formation of Dry Spots on Cornea. J Coll Interface Sci, 1985;106, 12–27.
Sharma A, Khanna R, Ruckenstein E. A thin film analog of the corneal mucus layer of the tear film: an enigmatic long range non-classical DLVO interaction in the breakup of thin polymer films. Coll Surf B: Biointerfaces, 1999;14, 223–235.
Zhang L, Matar OK, Craster RV. Analysis of tear film rupture: Eect of non-Newtonian rheology. J Coll Interface Sci, 2003;262, 130–48.
Begley CG, Simpson T, Liu H, Salvo E, Wu Z, Bradley A, et al. Quantative Analysis of Tear Film Fluorescence and Discomfort During Tear Film Instability and Thinning. Invest Ophthalmol Vis Sci, 2013;54, 2645–2653.
Begley CG, Himebaugh N, Renner D, Liu H, Chalmers R, Simpson T, et al. Tear breakup dynamics: a technique for quantifying tear film instability. Optom Vis Sci, 2006;83(1): 15–21.
King-Smith PE, Reuter KS, Braun RJ, Nichols JJ, Nichols KK. Tear film breakup and structure studied by simultaneous video recording of fluorescence and tear film lipid layer images. Invest Ophthalmol Vis Sci, 2013;54(7): 4900–4909.
Peng CC, Cerretani C, Braun RJ, Radke CJ. Evaporation-driven instability of the precorneal tear film. Adv Coll Interface Sci, 2014;206, 250–264.
Braun RJ, Driscoll TA, Begley CG, King-Smith PE, Siddique JI. On tear film breakup (TBU): dynamics and imaging. Math Med Biol, 2018;35(2): 145–180.
Zhong L, Ketelaar CF, Braun RJ, Begley CG, King-Smith PE. Mathematical modelling of glob-driven tear film breakup. Math Med Biol, 2018;36(1): 55–91.
Luke RA, Braun RJ, Driscoll TA, Awisi-Gyau D, Begley CG. Parameter Estimation for Mixed-Mechanism Tear Film Thinning. Bull Math Bio, 2021;83(56): Available from: https://doi.org/10.1007/s11538-021-00871-x.
Braun RJ, Driscoll TA, Begley CG. Mathematical Models of the Tear Film. Ocular Fluid Dynamics. Springer, 2019; 387–432.
Braun RJ, Gewecke NR, Begley CG, King-Smith PE, Siddique JI. A model for tear film thinning with osmolarity and fluorescein. Invest Ophthalmol Vis Sci, 2014;55(2): 1133–1142.
Winter KN, Anderson DM, Braun RJ. A model for wetting and evaporation of a post-blink precorneal tear film. Math Med Biol, 2010;27, 211–225.
Braun RJ. Dynamics of the tear film. Annu Rev Fluid Mech, 2012;44, 267–297.
Luke RA, Braun RJ, Driscoll TA, Begley CG, Awisi-Gyau D. Parameter Estimation for Evaporation-Driven Tear Film Thinning. Bull Math Bio, 2020;82(6): Available from: https://doi.org/10.1007/s11538-020-00745-8.
Gilbard JP, Farris RL, Santamaria J. Osmolarity of tear microvolumes in keratoconjunctivitis sicca. Arch Ophthalmol, 1978;96(4): 677–681.
Craig JP, K NK, Nichols JJ, Caffery B, Dua HS, Akpek EK, et al. The TFOS DEWS II Definition and Classification Report. Ocul Surf, 2017;15, 276–283.
Tomlinson A, Doane M, McFadyen A. Inputs and Outputs of the Lacrimal System: Reviewof Production and Evaporative Loss. Ocul Surf, 2009;7(4): 186–198.
Stahl U, Willcox M, Stapleton F. Osmolality and tear film dynamics. Clin Exp Optom, 2012;95(1): 3–11.
Braun RJ, King-Smith PE, Begley CG, Li L, Gewecke NR. Dynamics and function of the tear film in relation to the blink cycle. Prog Retin Eye Res, 2015;45, 132–164.
Lemp MA, Bron AJ, Baudouin C, Castillo JMB del, Geffen D, Tauber J, et al. Tear osmolarity in the diagnosis and management of dry eye disease. Am J Ophthalmol, 2011;151(5): 792–798.
Tomlinson A, Khanal S, Ramaesh K, Diaper C, McFadyen A. Tear film osmolarity: determination of a referent for dry eye diagnosis. Invest Ophthalmol Vis Sci, 2006;47(10): 4309–4315.
Versura P, Profazio V, Campos E. Performance of tear osmolarity compared to previous diagnostic tests for dry eye diseases. Curr Eye Res, 2010;35(7): 553–564.
Sullivan BD, Whitmer D, Nichols KK, Tomlinson A, Foulks GN, Geerling G, et al. An objective approach to dry eye disease severity. Invest Ophthalmol Vis Sci, 2010;51(12): 6125–6130.
Dartt D, Willcox M. Complexity of the tear film: importance in homeostasis and dysfunction during disease. Exp Eye Res, 2013;117, 1–3.
Liu H, Begley C, Chen M, Bradley A, Bonanno J, McNamara NA, et al. A Link between Tear Instability and Hyperosmolarity in Dry Eye. Invest Ophthalmol Vis Sci, 2009;50, 3671–79.
Pflugfelder SC. Tear dysfunction and the cornea: LXVIII Edward Jackson memorial lecture. Am J Ophthalmol, 2011;152(6): 900–909.
Belmonte C, Acosta MC, Merayo-Lloves J, Gallar J. What causes eye pain? Curr Ophthalmol Rep, 2015;3(2): 111–121.
Nichols JJ, Mitchell GL, King-Smith PE. Thinning rate of the precorneal and prelens tear films. Invest Ophthalmol Vis Sci, 2005;46(7): 2353–2361.
Kimball SH, King-Smith PE, Nichols JJ. Evidence for the major contribution of evaporation to tear film thinning between blinks. Invest Ophthalmol Vis Sci, 2010;51(12): 6294–6297.
Hamano H, Hori M, Mitsunaga S. Measurement of evaporation rate of water from the precorneal tear film and contact lenses. Contacto, 1981;25(2): 7–15.
Peng CC, Cerretani C, Li Y, Bowers S, Shahsavarani S, Lin M, et al. Flow evaporimeter to assess evaporative resistance of human tear-film lipid layer. Ind Eng Chem Res, 2014;53(47): 18130–18139.
Dursch TJ, Li W, Taraz B, Lin MC, Radke CJ. Tear-film evaporation rate from simultaneous ocular surface temperature and tear-breakup area. Optom Vis Sci, 2018;95(1): 5–12.
Awisi-Gyau D. Characterization of tear breakup and its sensory effects. PhD Thesis, Indiana University, 2020; 1–202.
Carlson NB, Kurtz D, Hines C. Clinical procedures for ocular examination. 3. New York: McGraw-Hill, 2004; 1–487.
Webber WRS, Jones DP. Continuous Fluorophotometric Method Measuring Tear Turnover Rate in Humans and Analysis of Factors Affecting Accuracy. Med Biol Eng Comput, 1986;24, 386–392.
Mota M, Carvalho P, Ramalho J, Leite E. Spectrophotometric analysis of sodium fluorescein aqueous solutions. Determination of molar absorption coefficient. Int Ophthalmol, 1991;15(5): 321–326.
Tiffany JM. The viscosity of human tears. Int Ophthalmol, 1991;15(6): 371–376.
Nagyová B, Tiffany J. Components responsible for the surface tension of human tears. Curr Eye Res, 1999;19(1): 4–11.
Wu Z, Begley CG, Port N, Bradley A, Braun R, King-Smith E. The effects of increasing ocular surface stimulation on blinking and tear secretion. Invest Ophthalmol Vis Sci, 2015;56(8): 4211–4220.
Nocedal J, Wright S. Numerical optimization. Berlin: Springer Science & Business Media, 2006; 1–597.
LeVeque RJ. Finite Dierence Methods for Ordinary and Partial Differential Equations: Steady-State and Time-Dependent Problems. Philadelphia: SIAM, 2007; 1–339.
Howell P. Models for thin viscous sheets. Euro J Appl Maths, 1996;7, 321–343.
Wolffsohn JS, Arita R, Chalmers R, Djalilian A, Dogru M, Dumbleton K, et al. The TFOS DEWS II Diagnostic Methodology Report. Ocul Surf, 2017;15, 544–579.